Grafy a regresní model
- Robert, vaRcraft
- 13. 11. 2016
- Minut čtení: 10
V minulém díle, jak si určitě mnozí z Vás pamatují, jsme se podívali na základy datového zpracování v R – import dat, jejich počáteční inspekce, jednoduché transformace a tvorba datových objektů přímo v kódu. Tento díl má za úkol přiblížit čtenářům již definici samotného modelu MNČ (anglicky OLS), jak počáteční, tak i inspekční vizualizaci dat, diagnostiku výstupů odhadu modelů a jejích případné využití pro další úlohy.
Začneme ale ještě úvodem do časových řad, neboť se jedná o častý typ vstupních dat pro ekonometrické modelování a vyžadují v R poněkud „osobní“ přístup, aby fungovaly korektně a pohodlně.
Představte si, že máte nějakou časovou řadu hodnot, např. jako v kódu a na obrázku níže. Vidíte, že při jejím grafickém vykreslení, nedokážeme z grafu poznat o jaké pozorování (v jakém čase) se přesně jedná. Jen, utíkajíc trochu dopředu, uvedu, že k základní vizualizaci slouží funkce plot (). Podrobněji vysvětlíme níže.

Jak je vidět na obrázku výše, graf jednak je defaultního typu bodový, což u časové řady nedává tolik smysl. Jednak je těžké odečítat hodnoty a informace, protože na ose X je jen automaticky nagenerovaný index záznamů, tedy čísla od 1 do N. Naše proměnná, kterou jsme vizualizovali, v sobě nenese žádné upřesňující informace - graf nemá odkud tuto informaci získat. Pro vyřešení neduhu formátujeme objekt jako ČŘ. To se v R uskutečňuje pomocí funkce ts(). Doplňkem, jak už to bývá u podobných funkcí, jsou funkce as.ts() (konvertovat) a is.ts() (ověřit, zda je objekt tohoto typu). Z parametrů funkce Vám postačí znalost těchto:
Ostatní parametry a jejích vysvětlení můžete zjistit příkazem ?ts v příkazovém řádku v RStudio. Pokračujeme v předchozím příkladu a konvertujeme proměnnou na ČŘ.
Pokud opět spustíme příkaz plot(numjobs), pak uvidíme následující výstup v grafickém okně:

Vidíme tedy, že graf je najednou čárového typu, aniž bychom nějak měnili parametry funkce plot(). Rovněž je pod osou X titulek Time a popisky ose nesou informaci, o jaký časový okamžik (měsíc) se jedná. Zatím to vypadá nešikovně, interval mezi popisky je moc široký, ale lze to jednoduše ovlivnit.
Proč se všechny tyto atributy najednou „samovolně“ změnily? Protože funkce plot() identifikovala, že vstupní objekt je typu ts (time series), tedy pro vizualizaci vyvolala svoji mutaci plot.ts(), k níž patří čárový typ grafu a u které se automaticky předpokládá, že vizualizujete něco v čase - proto Time. Ostatní změny plynou z informací, které již jsou v objektu numjobs uloženy a tedy popisky pozorování (a samotný typ objektu). Podívejme se na atributy objektu numjobs:
V atributu tsp vidíme údaje o prvním a posledním časovém okamžiku zapsanými v číselné podobě a parametr frequency. Jelikož je 1/12 = 0.08333 a leden je značen 0, pak je logické, že prosinec značí číslo 11*1/12=0.9166667. V atributu class pak vidíme hodnotu ts, která i určuje, že se jedná o časovou řadu.
Pojďme si teď vysvětlit funkci plot(). Jedná se o obecnou vizualizační funkci, která je schopná vykreslit velké množství nejrůznějších R objektů různých tříd a typů. Nejdůležitější parametry jsou samozřejmě pro definici vstupních dat pro graf. Pokud chcete vizualizovat jen jednu proměnnou, stačí jen napsat plot(numjob), pokud však chcete vytvořit tzv. X-Y plot, tak musíte zadat, která proměnná má být na ose X, která na ose Y. K tomu slouží stejnojmenné parametry x a y. Tedy můžeme definovat jako plot(rnorm(100), runif(100)).
Většina parametrů funkce pochází ze skupiny grafických parametrů par, uvedeme si na začátek jen několik nejdůležitějších z nich.
Ostatní parametry můžete prozkoumat po zadání ?par v příkazovém řádku, skupinu grafických parametrů čítá desítky atributů. My budeme dále používat jen několik z nich, proto nám výše uvedený seznam postačí.
Regresní model
Začneme s konstrukci regresního modelu a všemi procedurami, které by tomu měly předcházet a následovat.
Pro naši ukázku budeme potřebovat nějaký dataset a pro jednoduchost použijme jeden z těch v balíčcích standardně nabízených. Budeme pracovat s daty mtcars. Spusťte tedy kód
data(mtcars)
Následně zkuste zobrazit základní přehled o datech funkcí summary(mtcars). Jednak se dozvíte, které proměnné dataset obsahuje, jednak už uvidíte jejích základní popisné charakteristiky. Jak už jsme probírali v minulých lekcích, poněkud alternativně můžete použít str(mtcars), kde se rovněž dozvíte názvy proměnných a jejich datový typ (popisné charakteristiky už ne). Přečíst si nápovědu k dostupných v balíčcích datasetům můžete opět pomoci dotazu např. ?mtcars.
Zkusíme si tedy podívat na pár proměnných v datasetů a vykreslit si je na grafech. Nejdřív si zkusíme podívat na spotřebu vozů v datasetu, která je vyjádřena na americký způsob ukazatelem MPG (miles per gallon). Chceme bodový graf červené barvy, s nadpisem MPG plot, osou Y nadepsanou mpg a bez nadpisu osy X. Nejdřív však zkuste jen příkaz:
plot(mtcars$mpg)
adresování sloupců/proměnných v data frame jsme již probírali v minulých příspěvcích, ale kdybyste je ještě neviděli, tak se podívejte např. sem. Pokud je Vám jasné, proč je tam symbol dollarů, pokračujeme dál. Teď zkuste upravit příkaz pro graf tak, aby odpovídal výše popsanému požadavku.
Výstup takového příkazu musí vypadat jako na obrázku níže.

Jelikož však nemáme zda data v podobě časových řad, tak jednorozměrné zkoumání samo o sobě nepředstavuje nijak zásadní nebo zajímavou informaci. Spíše nám pomohou k získání nějakých informací tzv. X-Y ploty. Zkusíme tedy přepsat kód posledního grafu tak, abychom se podívali na závislost spotřeby na objemu motoru (zde opět v amerických jednotkách, tedy kubických palcích) – atribut disp. Samozřejmě, chceme upravit i nadpisy os, hlavní nadpis grafu a také použijeme parametr pch, protože chceme zobrazit křížky místo kroužků (bodů). Předpis musíme upravit následujícím způsobem:
O něco hezčí a hlavně víc informačně přínosný graf získáme v této podobě:

Teď zkusíme prozkoumat další závislost a to čas na 402 m a výkon v koních. Také zkusíme zobrazení pomoci plných bodů, změníme trochu barvu, tentokrát specifikujeme pomocí hexadecimálního kódu a samozřejmě definujeme odpovídající názvy grafů a os.
Ve výsledku dostáváme

Zkuste teď nějaký jiný pár proměnných, které dle Vás dávají smysl (nebo i nedávají, pokud auta Vám moc neříkají ;)) a také vyzkoušet jiné barvy, typy zobrazení a nadpisy.
Histogram
Určitě byste také měli umět vytvořit histogram v Rku, čehož lze dosáhnout několika způsoby. Tím nejjednodušším (ale také s nejméně pohledným výstupem) je základní funkce hist(). Vytvoříme histogram proměnné qsec:
hist(mtcars$qsec)

Hustotu pravděpodobnosti pak můžete vykreslit např. použitím těchto dvou funkcí (jistě, jako obvykle je způsobu mnohem více):
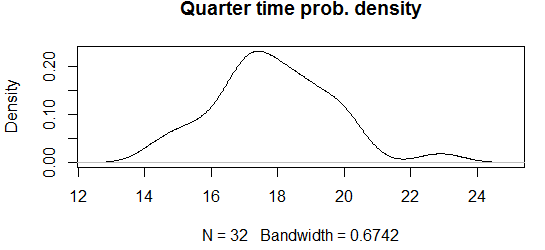
plot(density(mtcars$qsec), main="Quarter time prob. density")
Jsou ale hezčí a šikovnější způsoby, které demonstrujeme v jednom z dalších příspěvků.
K samotnému modelu - korelace
Jako první při konstrukci lineárního modelu byste měli prozkoumat korelace mezi vysvětlujícími proměnnými. To můžete v R realizovat pomoci funkce cor(). Důležitými parametry jsou
cor(x=mtcars$mpg, y=mtcars$cyl)
Lze vidět, že výstup je vracen ve formě matice, kdy řádky a sloupce přísluší jednotlivým proměnných a elementy v jejich průsečíku představují samotné korelační koeficienty. Tak např. lze odvodit, že korelační koeficient mezi objemem motoru a počtem válců je roven 0.9, mezi objemem a výkonem 0.79 atd. Tato forma výstupu však není příliš komfortní zejména pro větší datasety, takže se hodí ji nějak transformovat. Jak, si ukážeme v příštím díle, kde pomoci vlastní funkce s parametry nadefinujeme jen takový výstup korelační matice, který budeme chtít.
Když už víme, jak vypadá korelační matice, které vysvětlující proměnné bychom tedy neměli zahrnout do modelu spolu a že všechny proměnné jsou numerické, můžeme přistoupit ke konstrukci modelu.
Pro odhad lineárního modelu v R použijeme funkci lm(). Funkce rovněž slouží pro odhad rozptylu a kovarianční analýzu (i když funkce aov() disponujeme komfortnějším interfacem pro tento účel). Nejdůležitější parametry prozkoumáme opět v tabulce:
Sestavení a odhad modelu
Teď, když už umíme specifikovat příkaz pro odhad MNČ, zkusíme odhadnout model pro data mtcars. Z korelační matice plyne, že do modelu nemůžeme zařadit kombinace proměnných disp a cyl, hp a cyl, vs a cyl a wt a disp. Budeme si muset vystačit jen s jednou proměnnou z páru.
Zkuste spustit následující kód:
Specifikovali jsme požadovaný model, uložili jeho výstup do objektu lm a pak příkazem summary(lm) zobrazily výstup. Ten by měl vypadat takto:
Kdybyste nepoužili funkci summary a zkusili získat výstup rovnou voláním objektu lm, tak by výstup byl značně méně obsáhlý (zkuste si to). U některých funkcí (odhadu modelu) to ale funguje přesně naopak, proto to chce vyzkoušet.
Teď k samotnému výstupu: zcela nahoře vidíme opět tzv. call – čili předpis modelu, pod tím vidíme základní charakteristiky reziduí (proč chybí průměr a jaký by měl být?) a dále už odhad samotných regresních koeficientů, jejich standardní chyby, p-hodnoty. Pod tabulkou s regresními koeficienty můžeme najít celkové charakteristiky modelu jako koeficienty determinace, F-statistiku a její p-hodnotu (resp. významnost modelu jako celku).
V tomto případě lze odvodit, že jedinou významnou proměnnou na 5% hladině významnosti kromě konstanty je váha automobilu, která má signifikantní vliv na spotřebu. Výkon je signifikantní na 10 %, ostatní proměnné nejsou ani na této hladině (neberte výsledky nijak směrodatně, soubor obsahuje pouze 32 pozorování a rovněž lze očekávat nelineární vliv některých proměnných – model je pouze pro ukázku). Teď se podíváme, co všechno lze z takto odhadnutého modelu „vydolovat“.
Atributy modelu lm
Atributy získáme již známým příkazem attributes(lm). V příkazovém řádku uvidíme následující výstup.
Sekce $names obsahuje názvy podobjektu (atributů) modelu lm, kde vidíme např. zvlášť vektor koeficientů - coefficients, vektor reziduí - residuals, vektor vyrovnaných (odhadovaných) hodnot – fitted.values, samotný předpis funkce - call, a samotná vstupní data (pod atributem model). Ostatní atributy si můžeme dostudovat na help stránce ?lm. Volání atributů se odehrává jako vždy přes „dolar“, např. lm$fitted.values.
Diagnostika modelu
Po nalezení modelu, který dává smysl a má akceptovatelnou přesnost, musíme provést jeho diagnostiku: testy na autokorelaci, heteroskedasticitu (příp. multikolinearitu), eventuálně na správnost specifikace nebo normalitu reziduí.
Autokorelace
Testovat autokorelaci v tomto případě nemá velký smysl, neboť se nejedná o časové řady. Lze jen stěží předpokládat, že pozorování předcházejícího automobilu je významně zkorelováno s tím následujícím, těžko lze tady provést i volbu testovaného zpoždění (dle čeho se volí zpoždění v časových řadách?). Pro ukázku však test provedeme:
Použili jsme dvě různé funkce, Box.test (balíček stats, načítá se automaticky) a bgtest z balíčku lmtest, který je potřeba dodatečně načíst v kódu. Ve funkci Box.test je na výběr test Ljung-Boxův a Box-Piercův. Funkce bgtest představuje známý Breusch-Godfrey test.
Hlavním rozdílem ve specifikaci je zadání vstupu, který v případě Box.testu vyžaduje jen konkrétní testovanou řadu (tedy rezidua odhadnutého modelu), kdežto bgtest vyžaduje specifikaci objekt typu formula nebo lm object (celý odhadnutý model).
Heteroskedasticita
Použijeme např. Breusch-Pagan test, který má v R cekem intuitivní předpis: bptest(formula nebo lm objekt), v našem případě vypadá tedy jako bptest(lm).
Hodnota je sice těsně nad 0,05, ale přesto H0 o homoskedasticitě neodmítneme a konstatujeme tedy neporušení předpokladu.
Multikolinearita
Multikolinearitě částečně předcházíme už tak, že pečlivě vybíráme vysvětlující proměnné na samém začátku pomoci zkoumání párových korelačních koeficientů v korelační matici, ale přesto je dobré provést následně testy po odhadu modelu. Asi nejpopulárnější metodou, aplikovanou na výsledek modelu, jsou tzv. inflační faktory rozptylu, nebol-li anglicky variance inflation factors (VIF). Podrobněji si o tom můžete přečíst např. zde https://onlinecourses.science.psu.edu/stat501/node/347.
Ve zkratce jde o míru, vyjadřující, o kolik je rozptyl odhadovaného koeficientu proměnné nadhodnocen kvůli multikolinearitě s ostatními proměnnými. Míra (číslo) tedy vyjadřuje, kolikrát je vyšší, než minimálně dosažitelná teoretická mez.
R poskytuje výpočet VIF např. v balíčku car, pod funkci vif. V našem příkladu použijeme jako
Pokud hodnoty VIF překročí 4 resp., pokud hodnota odmocniny VIF překročí hodnotu 2, pak je proměnnou vhodné vynechat, neboť existuje nezanedbatelná statistická vazba mezi danou proměnnou a jednou či několika (lineární kombinace) jiných proměnných. V tomto případě máme problém s proměnnými wt, gear a carb.
Nutno dodat, že pokud se multikolinearita neblíží perfektní a netlačí determinant matice (X'X)^-1 k nule, o čemž Vás R bude při odhadu informovat hláškou Near-singular matrix, tak multikolinearita nepředstavuje zásadní problém pro predikční model. Z toho důvodu, že vzájemné závislosti proměnných lze i nadále očekávat v podobné síle a směrech, takže takový model bude při prognózování lepší, než kdybychom problematické proměnné vynechali.
Normalita reziduí
Pro testování normality lze vybírat z celkem široké škály testů, nicméně síla a kvalita některých z nich se v odborné literatuře zpochybňuje, nebo se poukazuje na jejich nevýhody pro některé konkrétní příklady použití. V poslední době se častěji kritizuje celkem rozšířený Jarque-Bera test. Stejné typy testů normality můžete také najít v různých balíčcích. Již zmíněny test Jarque-Bera se tak např. nachází v balíčku moments, vars, ccgarch, tseries a fBasics.
Ukážeme si několik testů a grafickou pomůcku. Níže umístím už rovnou kód a výsledky, použijeme sadu testů NormalityTests z balíčku fBasics:
Nulová hypotéza testů je formulováno jako „řada má normální rozdělení“. Z uvedeného je vidět, že výsledky se poněkud různí, je to ale dáno nejspíše tím, že máme málo pozorování a rozdělení je opravdu „na hraně“, jak uvidíme níže na qqplotu. V tomto případě je to jedno, v praxi spíš platí výsledek většiny testů (tedy nulovou hypotézy normality neodmítneme). U testu Kolmogorov-Smirnov je potřeba se dívat na two-sided hypotézu.
Zmíněný qqplot představuje dobrou grafickou pomůcku, neměli byste ale z něj nic odvozovat jistě, pamatujte, že u všech testů hraje velkou roli počet pozorování! V R ho můžete jednoduše vytvořit pomoci funkce qqline():
qqline(lm$residuals)
Graficky výstup není nikterak pohledný, ale informativní ano:

Řada velmi blízká normálnímu rozdělení musí těsně kopírovat přímku na grafu (kterou právě tvoří teoretické normální rozdělení), v tomto případě vidíme „tlustší“ konce, protože se nám v horní a dolní části body od přímky vzdalují. Pokud bychom viděli stejný obrázek u řady s velkým počtem pozorování, šlo by prakticky s jistotou tvrdit o porušení normality.
Grafická diagnostika modelu
Když už model dává např. logický smysl, dobře vychází diagnostické testy a i kvalita vyjádřena např. R-sq se Vám líbí, přichází čas to pořádně okouknout. Základními grafy kromě qqplotu, které je dobré prozkoumat, jsou grafy reziduí, skutečných vs. odhadovaných hodnot a v případě odhadu časové řady určitě ACF a PACF. Postupně si ukážeme, jak se k nim dostat.
Graf reziduí je celkem jednoduchý, stačí použít již vysvětlenou funkci plot() a doladit už jen vzhled a typ zobrazení. Lze tedy použít např.

Z toho budete moct rozpoznat případnou autokorelaci nebo heteroskedasticitu, příp. závislost hodnot na pozorováních (nebo v čase). Modrá tečkovaná čára vykresluje střední hodnotu reziduí, která musí být vždy nulová (alespoň limitně).
Graf actual-fitted můžete získat pomoci dvou příkazů:

Kromě dvou příkazů máme ještě jeden pro vytvoření legendy – návod k legendě viz opět ?legend. Z takového grafu můžete, samozřejmě, odvodit, na kolik dobře a kde přesně se model trefuje/netrefuje do skutečných pozorování, která měl modelovat. Často zrovna při pohledu na tento graf Vás napadá, že asi něco v modelu není v pořádku, že tam možná chybí proměnná apod. Při vizuální podobě výstupy již se zapojuje intuice a cit na modelování (pokud ho, samozřejmě, máte). Proto je dobré kromě tvrdých čísel z testu se také dívat i na graf.
ACF a PACF
ACF a PACF jsou zkrácené názvy autokorelační a parciální autokorelační funkce, více se o tom můžete přečíst např. tady https://www.mathworks.com/help/econ/autocorrelation-and-partial-autocorrelation.html?requestedDomain=www.mathworks.com. Primární slouží pro identifikaci autokorelační „přírody“ v časových řadách a určení správné specifikace složek ARIMA procesů. V našem případě je využijeme identifikaci, příp. ověření neexistence autokorelace v reziduích modelu. Použijeme funkce acf() a pacf(). Grafy a kód pak vypadají následovně:
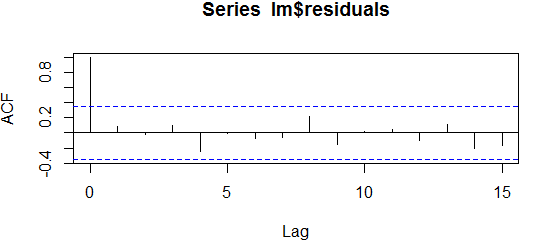

Správnost, resp. neexistenci autokorelaci poznáme tak, že žádný sloupeček (kromě toho prvního s indexem 0 v ACF, který je vždy roven 1) by neměl přesahovat přípustné meze vyznačené modrým „pasem“. V tomto případě vidíme, že jak již nám ukázaly testy, že autokorelace není přítomná.

V tomto příspěvku jsme se podívali na základy grafického zobrazení dat v R - jak různé typy jednorozměrných, tak i dvourozměrných (x-y) grafů a probrali základní atributy třídy par. Rovněž práci s časovými řadami a praktickým datasetem. Ten jsme využili ke konstrukci regresního modelu, čemuž předcházelo zkoumání párových korelačních koeficientů vysvětlujících proměnných. Po specifikaci a odhadu modelu jsme ukázali, jaké atributy obsahuje výstup odhadu lineárního modelu, jak je z tohoto výstupu získat a k čemu dalšímu použít. Vysvětlili jsme si diagnostiky odhadnutého modelu, podrobně probrali porušení předpokladů odhadu MNČ a ukázali jejich ověřování v R. Na konci jsme ukázali, jaké grafy je dobré po odhadu regresního modelu zkontrolovat.
Všechna táto témata představují základní instrumentárium datového analytika či ekonometra při práci s daty a konstrukci ekonometrických modelů. Zcela zásadní je i znalost funkcí a balíčků R, která obsahují / představují nutné funkcionality, testy a algoritmy. Grif však do ruky dostanete až postupným procvičováním, regulárním použitím a řešením nejrůznější problémů s vymyšlením vlastních řešení. Takže rada na konec: vzhůru do toho! :)





Komentáře