Matika a MNČ
- Robert, vaRcraft
- 7. 9. 2016
- Minut čtení: 3
Dnes si ukážeme ty nejjednodušší operace a základní dovednosti s objekty v Rku na příkladu odhadu MNČ (OLS) ručně krok po kroku. Rovněž Vám to připomene samotný výpočet a, pevně doufám, že mu nakonec porozumí i ti z Vás, kterým celou dobu unikal nebo se zdál poněkud zamlžený.
Základní matika
Jelikož základní matematické operace jako sčítání, odčítání, násobení a dělení určitě každý z Vás zvládne bez jakékoliv nápovědy, cvičení s nimi nechám jen na Vaší fantazii. Podíváme se tedy na ty „složitější“.
Níže budu používat často funkce seq(). Není to nic jiného, než generování sekvence čísel mezi zadaným maximem a minimem se zvoleným krokem – seq(1:5) produkuje řadu 1 2 3 4 5; seq(min=2, max=8, by=2) produkuje řadu 2 4 6 8.
Teď už k samotným operacím:
Pro další ukázky bude opět potřeba trochu obecnější teorie. Vysvětlíme si tedy pár datových typů a to vektory a matice.
Vektory
Vektor se v R vytvoří pomocí stejnojmenné funkce vector(). Vyžaduje dva vstupní parametry a to mode a length. Parametrem mode nastavujeme datový typ ukládaných dat a tedy celého vektoru a length R říká, z kolika prvků se musí vektor skládat.
Mode můžeme volit z následujících hodnot: "logical", "integer", "numeric" (synon. "double") , "complex", "character" a "raw". Nejčastěji využijete samozřejmě logical (TRUE/FALSE), integer/numeric a character.
Další mutací funkce vector(), jak je v R zvykem, je funkce as.vector(). Pro tu je potřeba zadat vstupní objekt, ze kterého se vektor vytvoří, a následně opět mode.
Vektory tedy můžete tvořit např. těmito dvěma způsoby:
Mezi nevýpočetní operace, které s vektory můžeme provádět a jsou často potřeba, patří cbind() a rbind(). Jak může být patrné z názvů, jde o sloupcové a řádkové řetězení. cbind() umístí dva vektory vedle sebe jako sloupce, rbind() naopak pod sebe jako řádky. POZOR: vektory musí mít stejnou velikost!
Pár příkladů:
Teď už umíte vektory vytvořit, naplnit hodnotami i provést některé transformace. Zvýšíme tedy dimenzionalitu o jedničku a podíváme se na logicky navazující datový typ - matice.
Matice
Co je matice, nejspíše většina z Vás dobře ví, proto pro podrobný popis odkážu na prostory internetu. Ve zkratce - je to dvoudimenzionální pole, obsahující nějaké prvky (čísla, znaky apod.), které jakýmsi způsobem vyjadřuje i jejich uspořádání či vzájemný vztah. V Rku je tvorba matice skoro úplně stejná jako tvorba vektorů - slouží k tomu funkce matrix() a as.matrix(). Parametr mode zde neuvidíte, avšak je vyžadován o jeden rozměrový parametr navíc: musíte poskytnout nrow a ncol (pokud nespecifikujete vstupní data, jinak stačí jeden z parametrů a druhý si R dopočítá). Na rozdíl od vektoru však můžete přímo specifikovat data, ze kterých se má matice vytvořit, již ve funkci matrix(). Bez uvedení atributu data R vygeneruje matici s NA hodnotami. Zajímavý je také atribut byrow, kterým R sdělíte, zda se matice má plnit řádkově, nebo sloupcově. Standardně se plní (možná trochu neintuitivně) sloupce, viz příklad níže:
Všechny ostatní operace si ukážeme a naučíme rovnou na praktickém příkladě, neboť zabijeme dvě mouchy jednou ránou a bude se to "situačně" i líp pamatovat.
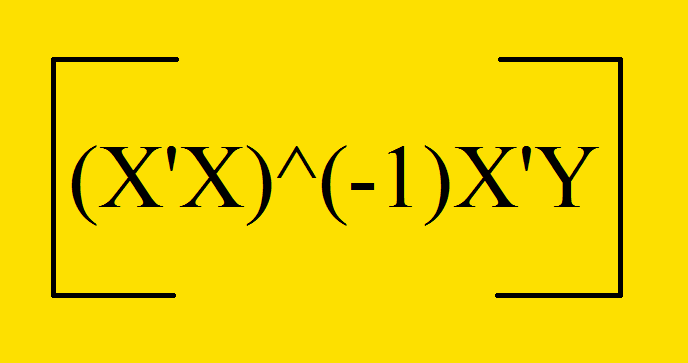
MNČ / OLS (Ordinary Least Squares)
V závěrečné části si ukážeme příklad výpočtu metody nejmenších čtverců krok po kroku ("ručně") tak, jak to software i vykonává. Jak si možná pamatujete z kurzu ekonometrie, vzorec pro odhad parametrů vypadá následovně:
Pro výpočet výsledku, když máme hodnoty vysvětlujících i vysvětlované proměnné, potřebujeme kromě násobení jen dva další výpočty z daných matic - transpozici a inverzi. Jak to provést v R? Demonstrujeme rovnou kódem:

Uváděné výše funkce a operace patří k tomu nevyhnutelnému základu, který datový analytik, využívající R, potřebuje ke své práci a k vykonání nezbytných výpočtů, operací a datových transformací. Ruční výpočet MNČ pak připomíná všem zájemcům o ekonometrii, jak přesně metoda vypočítá parametry a jaké operace se v rámci toho odehrávají, což by mělo vést k lepšímu pochopení metody (a v praxi získávaných výsledků) nebo i dopadů např. porušení předpokladů MNČ. Pokud hodnost matice X (resp. X'X) není plná, pak nebude existovat ani inverzní matice a logicky ani odhad parametrů (multikolinearita).





Komentáře